Tout commence avec l’aire du rectangle
L’aire du rectangle se calcule en faisant le produit :
Longueur \times largeur

De cette aire, on trouve l’aire du triangle rectangle
Un triangle rectangle est alors vu comme la moitié de l’aire du rectangle que l’on construit à l’aide des côtés de l’angle droit.
La longueur est alors appelée la base et la largeur la hauteur … mais c’est la même chose.
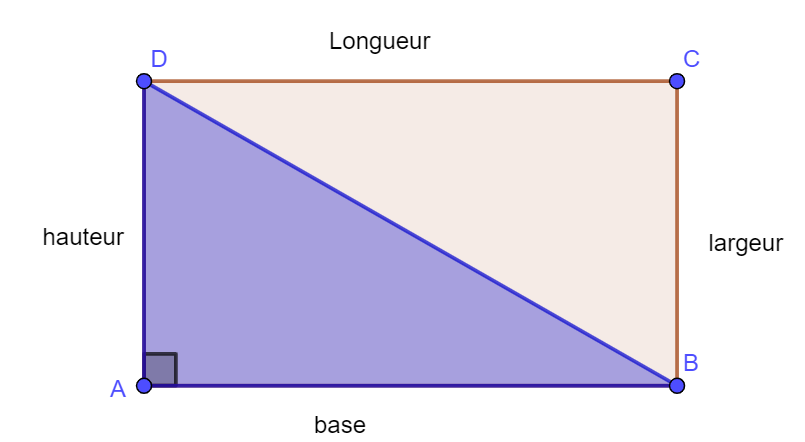
L’aire du triangle rectangle est bien la moitié de l’aire du rectangle ABCD.
Donc l’aire du triangle ABD rectangle en A est alors :
\dfrac{ base \times hauteur}{2} = \dfrac{AB \times AD}{2}
De l’aire du triangle rectangle on trouve l’aire de n’importe quel triangle.
Pour calculer l’aire du triangle AEB, on trace un rectangle en utilisant une base et la hauteur associée du triangle. Ici [AB] et [HE].
La hauteur du triangle est ici EH. Elle est perpendiculaire à la base choisie et passe par le sommet opposé.
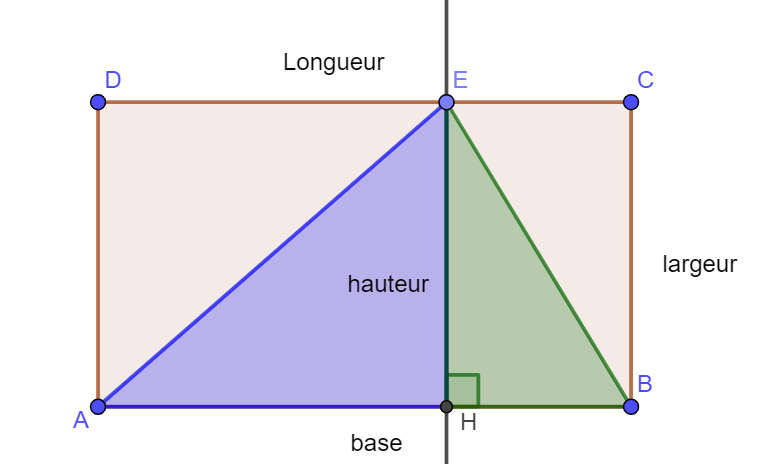
Dans cette construction, la hauteur partage le rectangle en 4 triangles rectangles et quand j’assemble le vert et le bleu pour former le triangle AEB, je peux voir que son aire est bien égale à la moitié de l’aire du rectangle donc l’aire du triangle AEB est donnée par :
\dfrac{ base \times hauteur}{2} = \dfrac{AB \times HE}{2}
La seule chose qui a changé ici par rapport au triangle rectangle c’est la place de la hauteur. Elle n’est plus un des cotés du triangle.
Les plus septiques ou les plus curieux me diront :
Mais quand la hauteur est en dehors du triangle … Comment fait-on ?
La réponse en image …

L’aire du triangle AEB est en rose.
J’ai pris [AB] comme base, la hauteur correspondante est [FE] et elle est bien à l’extérieur du triangle.
On construit toujours le rectangle dont la longueur est AB et la largeur BD (c’est toujours la hauteur du triangle …)
- L’aire du triangle rectangle EBF en bleu est bien la moitié de l’aire du rectangle BFED.
Je partage donc le rectangle en deux parties mais ici je le coupe horizontalement le long de la médiatrice de [FE].
On a donc l’aire de BFE = l’aire de HIDE.
- On regarde maintenant l’aire de ACE en vert, avec le rectangle AFEC, je constate la même chose :
l’aire de ACE= l’aire de AFIG
- Dans les deux figures le rectangle AFEC est le même.
C’est seulement son découpage qui a changé.
- Donc les aires vertes étant égales, les aires bleues étant égales, les aires rose le sont aussi…
Conclusion, l’aire du triangle ABE est bien la moitié de l’aire du rectangle dont un coté est égal à AB et l’autre à FE.
Mon calcul est toujours le même. L’aire du triangle AEB est donnée par :
\dfrac{ base \times hauteur}{2} = \dfrac{AB \times FE}{2}
De l’aire du rectangle à l’aire du losange
On va transformer notre losange en un rectangle tout en conservant son aire.
Le rôle des diagonales du losange est ici clair, la première devient la longueur du rectangle.
La largeur du rectangle est la moitié de la seconde diagonale du losange.
On utilise les diagonales du losange qui sont perpendiculaires pour le découper en 4 triangles rectangles superposables. On les assembles pour former le rectangle DTRB.

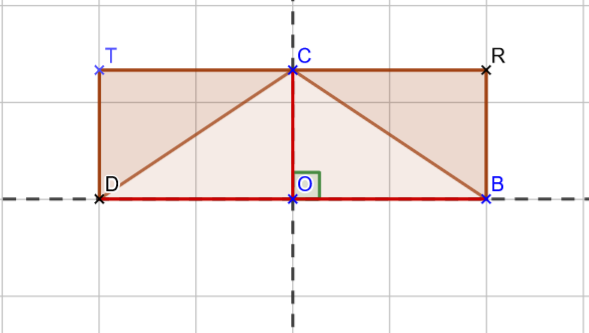
- La longueur est DB : la longueur de la première diagonale du losange.
- Sa largeur est CO : la moitié de CE, la seconde diagonale du losange.
Donc l’aire du losange est :
\dfrac{ petite \ diagonale \times Grande \ diagonale }{2} = \dfrac{DB \times CE}{2}
De l’aire du triangle à l’aire du parallélogramme

Sa diagonale le partage en 2 triangles superposables (car il possède un centre de symétrie).
Je sais déjà calculer l’aire du triangle ABE :
\dfrac{ base \times hauteur}{2} = \dfrac{AB \times HE}{2}
Celle du parallélogramme est son double donc :
base \times hauteur = AB \times HE
Le choix de la base est libre : le côté que je veux, comme pour le triangle.
La hauteur est ici la distance qui sépare la base du côté qui lui est parallèle.
De l’aire du triangle à l’aire du disque
On épluche le disque et on étale les morceaux pour en faire un triangle de même aire …
Dans cette animation nous montrons comment en épluchant le disque cercle par cercle, nous pouvons trouver l’aire du disque en construisant un triangle rectangle couche par couche.
A chaque étape, le périmètre du cercle rouge a la même longueur que le segment [MP]. Cela permet de construire le triangle AOC à partir de tous les cercles de centre O et de rayon OM.
On retiendra que l’aire du disque se calcule à l’aide de la formule :
\pi\times r\times r où r est le rayon du disque