I les triangles égaux
Définitions : Deux triangles sont égaux signifie qu’ils sont superposables.
Cas 1 : On connait les longueurs des 3 côtés du triangle. Le triangle que l’on peut ainsi construire est unique.
Exemple : Construire ABC avec AB = 7 cm, BC = 4 cm et AC = 6 cm.
Cas 2 : On connait les longueurs de 2 côtés du triangle et la mesure de l’angle formé par ses deux côtés.
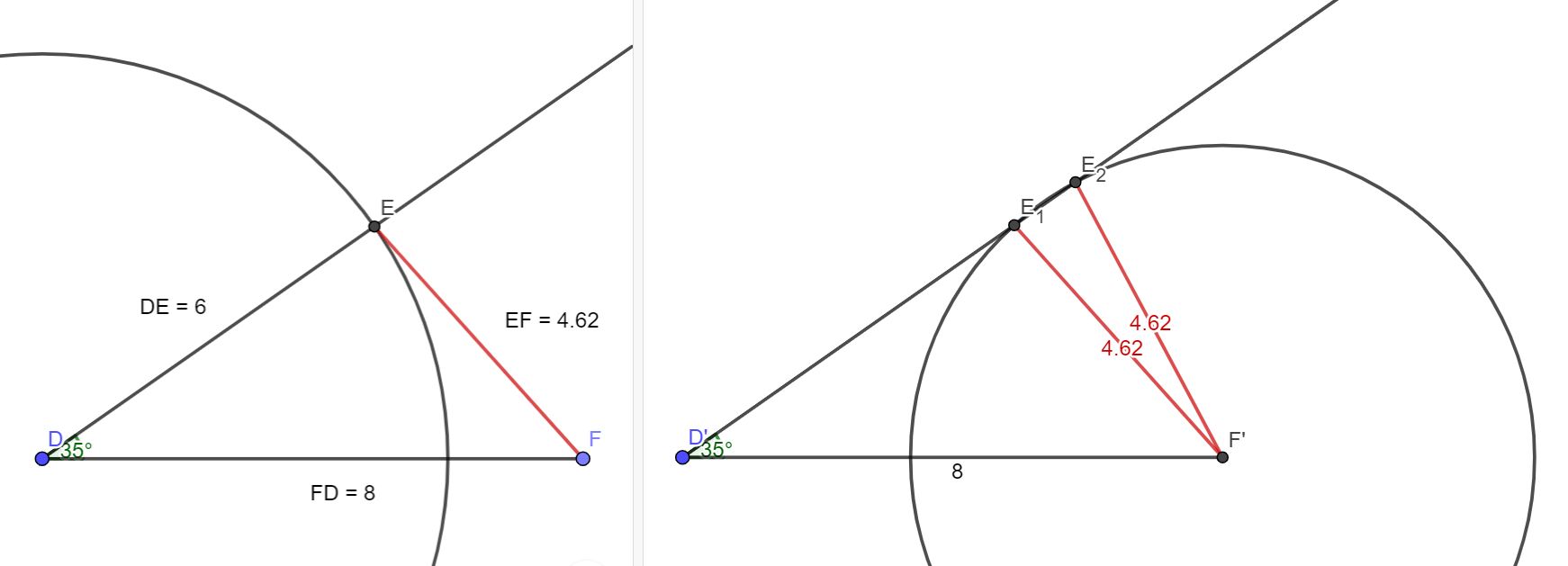
Exemple : Construire DEF avec DE = 6 cm, DF = 8 cm et \widehat{EDF} = 35°
A-t-on tous obtenu des triangles superposables ?
Quelle est la longueur du côté EF ?
Si on change l’énoncé en construire le triangle D’E’F’ avec D’F’ = 8 cm et et E’F’ = EF que se passe-t-il ? Obtient-on toujours un seul triangle ? \widehat{E'D'F'} = 35°
Cas 3 : On connait la longueur d’un segment et les mesures des deux angles dont les sommets sont les extrémités de ce segment.
Exemple : Construire SRT avec RS = 6 cm, \widehat{RST} = 75° et <code>\widehat{TRS} = 40°.
Dans ces 3 cas, les triangles que l’on obtient sont à chaque fois superposable. On dit qu’ils sont égaux.
II Les triangles semblables
Définition : Deux triangles sont semblables s’ils ont les mêmes mesures d’angles.
Dans la suite de cette partie on veut savoir comment savoir si deux triangles sont semblables sans toujours connaitre les mesures des angles. On veut aussi savoir si avec quelques longueurs on peut trouver celles qui correspondent dans un triangle semblable.
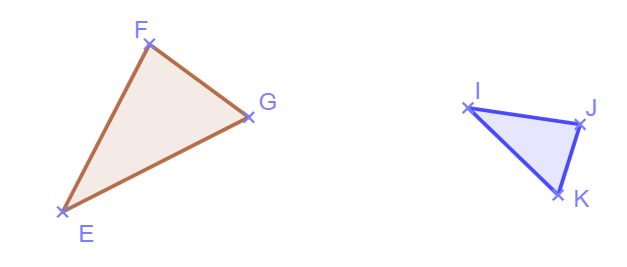
Les triangles EFG et IJK sont semblables. Les mesures des angles sont les mêmes.
On peut donc dire que deux triangles sont semblables si l’un est un agrandissement ou une réduction de l’autre.
Le problème est donc le suivant :
Si je connais les 3 longueurs des côtés d’un triangle, puis-je trouver les longueurs de l’autre triangle ?
A vous de mesurer les angles, les longueurs si besoin pour trouver une solution à ce problème dans tous les cas qui peuvent se produire.
Zoomer ou déplacer le point E si besoin pour voir les deux triangles.
Propriété : Lorsque deux triangles sont semblables, les côtés homologues sont dans le même rapport de proportionnalité.
Cela signifie que \dfrac{EF}{IJ}=\dfrac{FG}{JK}=\dfrac{GH}{KI} Dans cette égalité, les côtés [EF] et [IJ] sont homologues, les côtés [FG]et [JK] sont homologues et [GH] et [KI] le sont aussi. Cela signifie qu’il se correspondent après agrandissement ou réduction.
La réciproque de cette propriété est vraie.
Propriété : Lorsque dans deux triangles EFH et IJK, on a \dfrac{EF}{IJ}=\dfrac{FG}{JK}=\dfrac{GH}{KI} alors les triangles sont semblables.