Objectif : Réinvestir les connaissances sur les quadrilatères particuliers et justifier de leur nature et utilisant une propriété.
4 exercices vous sont ici proposés, à vous de les traiter.
Le dernier peut être fait avec GeoGebra pour être sûr d’avoir bien placé les points dans un repère.
Exercice 1 : On a tracé deux cercles de centre O de diamètres respectifs [AB] et [ED]. 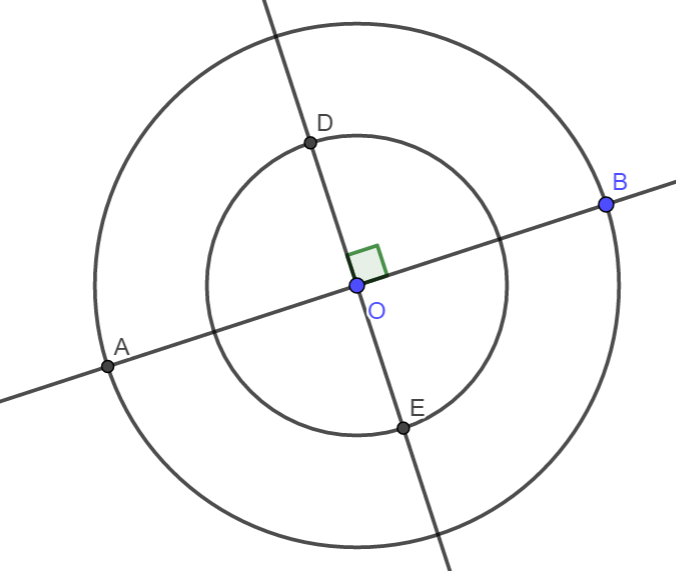
D’après les informations fournies par la figure et l’énoncé, quelle est la nature du quadrilatère AEBD ?
Quelle propriété vous permet de le justifier ?
Exercice 2 : R, I, M et E sont 4 points d’un même cercle de centre O. (On dit qu’ils sont cocycliques.).
D’après les informations fournies par la figure et l’énoncé, quelle est la nature du quadrilatère RIME ?
Quelle propriété avez-vous utilisé ?
Exercice 3 : Quelle propriété ?
Pour chaque affirmation, citer la propriété qui permet de la justifier.
- REST est un parallélogramme, donc les longueurs RE et ST sont égales.
- PRIX est un carré de centre O, donc O est le milieu de [RX].
- JOIE est un rectangle de centre C donc JC = OC.
- TRUE est un losange donc les droites (TU) et (RE) sont perpendiculaires.
Exercice 4 : Dans un repère orthonormé (axes perpendiculaires et même unité sur les deux axes), placer les points suivants :
A(5 ; 0), B( 3 ; 2 ), C( 1 ; 4 ),D( -2 ;-3) et E( 1 ; -2 ).
1. Placer les points F, R et T pour que
- BCFD soit un rectangle.
- BREA soit un parallélogramme.
- BEAT soit un losange.
2. Placer les centres de ces quadrilatères et donner les coordonnées de leurs centres par lecture graphique.
Un espace de travail GeoGebra est à votre disposition pour vous corriger ci-dessous. Avec un clic droit vous pouvez voir les coordonnées des points placés.
Vérifiez qu’ils sont bien placés et vérifiez ce que vous avez écrit sur votre cahier.