Objectif : Expliquer l’algorithme de la division posée et le visualiser à l’aide de GeoGebra.
Le support de cours est à recopier sur le cahier a fur et à mesure.
Vous disposez d’un fichier GeoGebra que vous pouvez utiliser pour faire des conversions qui vont permettre de répartir équitablement le gain en 23 personnes.
Pour faire les conversions, il faut former une phrase en remplissant les champs prévus à cet effet et en cliquant sur le bouton “valider” à votre disposition.
Pour vérifier votre conversion et voir si elle est possible, il faut utiliser le bouton “est-ce possible ?”. Suivant les cas, “le faire” ou “nouvelle proposition” vous sera proposé.
Vous pourrez alors visualiser votre conversion.
Par exemple, on peut convertir 2 dizaines de milliers en 20 milliers puisqu’il n’est pas possible de répartir 2 dizaines de milliers en en donnant 1 à chacune des 23 personnes.
On obtient alors 24 milliers que l’on peut répartir en 23 …
On peut vérifier à tout moment que le nombre est toujours le même avec la case “quel est ce nombre ?” changer son contenu pour ne plus avoir BRAVO ! écrit.
La division
I La division euclidienne
Dans une division euclidienne, il n’y a que des nombres entiers :
Le dividende, le diviseur, le quotient et le reste.
Par exemple, dans l’égalité, 73 = 11 \times 6 + 7,
73 est le dividende,
11 est le diviseur,
6 est le quotient et
7 est le reste.
Attention, le reste est toujours plus petit que le diviseur.
On ne peut donc pas dire que le reste de la division euclidienne de 73 par 6 est 7.
En effet, 73 = 6 \times 12 + 1, le reste de la division euclidienne de 73 par 6 est 1 et le quotient est 12.
II La division posée
Pour poser une division, on utilise une potence.
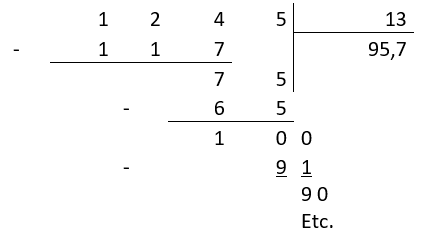
On considère 124 dizaines pour pouvoir les répartir en paquets de 13.
Dans 124 dizaines, il y a 9 \times 13 , dizaines soit 117 dizaines.
Il reste donc 124 – 117 = 7 dizaines que je ne peux pas répartir.
Je converti ces 7 dizaines en unités et je rajoute les 5 qui n’ont pas encore été utilisées dans 1245.
On dit que l’on abaisse le 5.
On considère 75 unités pour pouvoir les répartir en paquets de 13.
Dans 75 unités, il y a 5 \times 13 , unités soit 65 unités.
Il reste donc 75 – 65 = 10 unités que je ne peux pas répartir.
Je converti ces 10 unités en dixièmes. Cela me fait 100 dixièmes.
Mon quotient devient alors un nombre décimal (je cherche un nombre de dixièmes), il me faut donc rajouter une virgule après le 5 des unités du quotient.
Deux cas peuvent se produire.
- Je tombe sur un reste nul et donc la division s’arrête.
- Je tombe sur un reste que j’ai déjà rencontré,
la division sera infinie mais je sais quels chiffres du quotient vont se répéter.