Vous disposez d’un programme Scratch (en bas de cette page).
A l’aide de ce programme nous allons essayer de répondre à quelques questions.
Scratchy joue à un jeu dans lequel il se trouve au centre d’un labyrinthe.
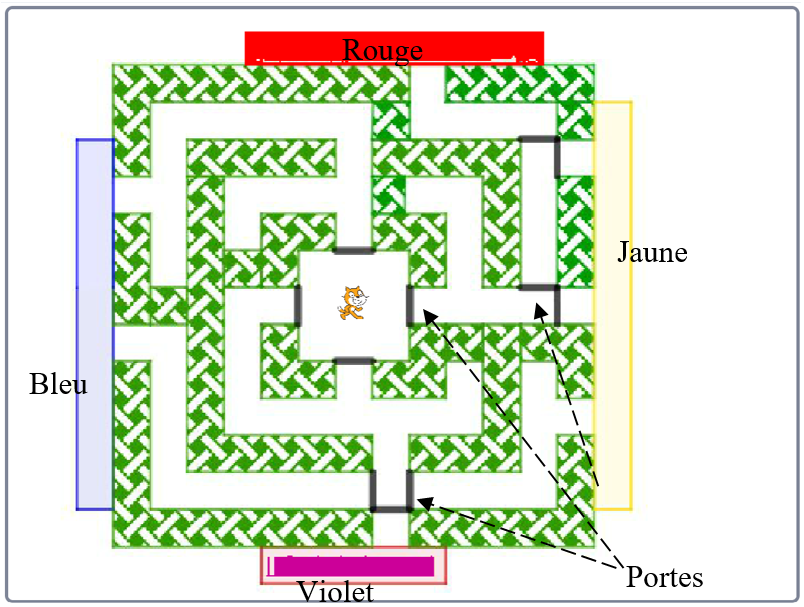
Il va devoir choisir au hasard une porte qui ne s’ouvre que dans un seul sens jusqu’à sortir par l’un des 4 chapiteaux (le rouge, le jaune, le violet et le bleu). Les portes sont toutes identiques et peuvent être ouvertes de manière équiprobable.
Emy, l’amie de Scratchy dispose de 4 cadeaux. Elle veut disposer un cadeau dans chaque chapiteau.
Les cadeaux dont elle dispose sont tous de valeurs différentes :
- un cerf-volant (20 €),
- un vélo (200 €),
- une place de concert (40 €),
- une tablette (340 €).
On cherche à savoir où placer les différents cadeaux.
Partie 1 : Répondre au problème à l’aide des statistiques
- A l’aide du programme fourni expliquer comment faire pour confirmer ou infirmer les propositions suivantes :
- Proposition 1 : « Il faut placer le cadeau le plus cher dans le chapiteau qui a le plus d’entrées »
- Proposition 2 : « Il faut placer le cadeau le plus cher dans le chapiteau qui a le plus de chemins qui y conduisent »
- Proposition 3 : « On peut placer n’importe quel cadeau dans n’importe quel chapiteau »
- Proposition 4 : « Il faut placer le cadeau le plus cher dans le chapiteau le plus grand »
- Comment disposer les cadeaux pour aider Scratchy à gagner le plus prestigieux des lots ? Justifier votre réponse en calculant la probabilité des évènements :
V = « Scratchy sort par le chapiteau violet »
R = « Scratchy sort par le chapiteau Rouge »
J = « Scratchy sort par le chapiteau Jaune »
B = « Scratchy sort par le chapiteau Bleu » - Paul a programmé ce jeu en Scratch et trouve les résultats suivants :
| Évènement | V | R | J | B |
| fréquence | 13 | 4 | 16 | 17 |
- Combien de parties a-t-il joué ?
- Pensez-vous que son jeu soit bien programmé ?
D’après « à vos maths », graphicor, 2005
Partie 2 : Vers le calcul de probabilités
Nous avons fait des statistiques en répétant plusieurs fois l’expérience et nous avons obtenu des résultats fluctuants (ils changent d’un échantillon à l’autre) mais nous avons dégagé résultats. Les deux chapiteaux que nous atteignons le plus souvent sont le bleu et le jaune. Ceux que nous atteignons le moins souvent sont le rouge et le violet.
Contrairement au pont des deux rives, nous pouvons ici calculer la probabilité de chaque évènement
B est l’évènement « scratchy atteint le chapiteau bleu »
J est l’évènement « scratchy atteint le chapiteau jaune »
R est l’évènement « scratchy atteint le chapiteau rouge »
V est l’évènement « scratchy atteint le chapiteau violet »
On numérote les différentes sorties de 1 à 10.
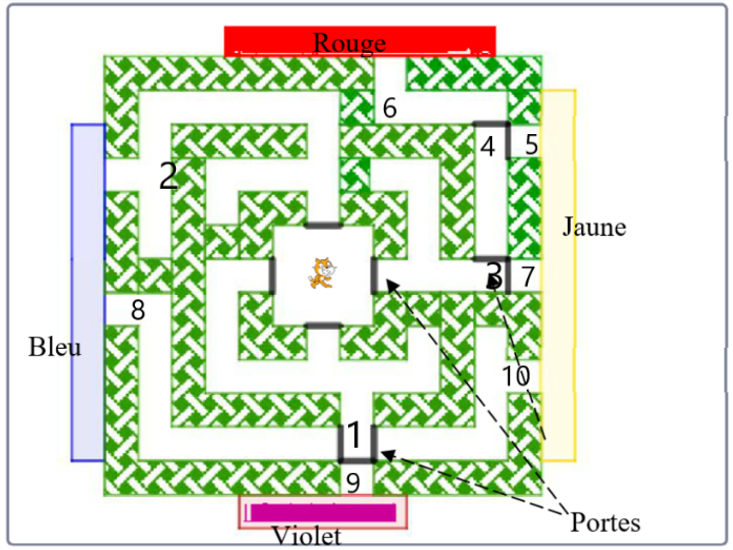
- Scratchy est au centre de la scène. A cause de l’équiprobabilité, combien de fois sur 300 essais, Scratchy va-t-il arriver en 1 ? En 2 ? En 3 ?
- Scratchy est en 1. Sur les … (utiliser la réponse de la question 1) de fois où scratchy est arrivé en 1 et toujours à cause de l’équiprobabilité, combien de fois va-t-il arriver en 8 ? en 9 ? en 10 ?
- Scratchy est en 3. Sur les … (utiliser la réponse de la question 1) de fois où scratchy est arrivé en 3 combien de fois va-t-il arriver en 7 ? en 4 ?
- Scratchy est en 4. Sur les … (utiliser la réponse de la question 1) de fois où scratchy est arrivé en 4 combien de fois va-t-il arriver en 5 ? en 6 ?
- Conclure en donnant sous forme d’écriture fractionnaire ou de fraction la probabilité des évènements B, R, J et V et répondre au problème de départ.