Objectif : Etablir les règles de priorités opératoires en lien avec l’écriture de calculs avec scratch.
Dans cette activité, écrite en 2018 avec l’introduction de Scratch au collège, nous revenons sur les priorités opératoires et la nature des expressions algébriques.
Vous devez répondre aux questions posées. Ces questions portent sur la nature des expressions algébriques, sur leur expression dans l’environnement Scartch et leur correspondance en mathématiques.
Le cours
Avec Scratch, c’est l’ordre de l’empilement qui donne les priorités : l’opérateur en haut de la pile est le calcul à effectuer en premier.
La nature de l’expression est alors visible puisqu’elle est portée par l’opérateur qui se trouve tout en bas de la pile.
Chaque opérateur est équivalent à une paire de parenthèses.
En mathématiques, nous avons d’autres règles qui permettent de ne pas écrire toutes les parenthèses.
Pour effectuer un calcul, je dois respecter des règles appelées : priorités opératoires.
Règles de priorités opératoires :
Dans une expression que je dois évaluer, je commence par :
- Les calculs entre parenthèses (et je réapplique cette règle depuis le début à l’intérieur des parenthèses).
- Les multiplications et les divisions sont prioritaires sur les additions et les soustractions.
- Quand il n’y a plus que des additions et des soustractions, je fais les calculs dans le sens de lecture et 1 par 1.
Remarque : C’est le dernier calcul effectué ou à effectuer (en respectant la règle ci-dessus) pour obtenir un résultat qui donne la nature d’une expression.
- Si c’est une addition on parle de somme et les nombres que l’on ajoute sont appelés des termes.
- Si c’est une soustraction, on parle de différence et les nombres avec lesquels on opère sont des termes.
- Si c’est une multiplication, on parle de produit et les nombres sont des facteurs.
- Si c’est une division, on parle de quotient et il y a un dividende et un diviseur.
Exemple :

A est une différence car la dernière opération à effectuer avant de trouver un résultat est une soustraction.
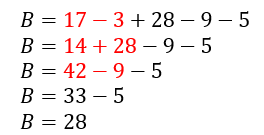
B est aussi une différence.
Remarque la partie 3 de la règle peut être adaptée :

- Deux calculs simultanés peuvent être prioritaires
- On considère alors le symbole opératoire devant le premier terme de la somme ou de la différence comme le signe de ce nombre et on peut ainsi modifier l’ordre des termes à condition de les déplacer avec le symbole opératoire qui précède chaque terme.
B = 14 + 14
B = 28
Ainsi B est aussi une somme.
On peut donc constater aussi que :
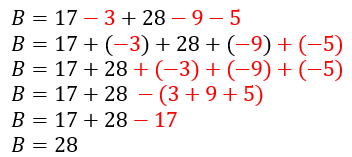
Ici c’est la règle de transformation d’une somme en une différence qui justifie les changements de priorité.
Propriété : Soustraire un nombre revient au même qu’ajouter son opposé.
Dans ce que nous avons fait soustraire 3 est équivalent à ajouter (-3).
Mais nous avons aussi utilisé qu’ajouter -17 est équivalent à soustraire 17